No.10 1998 中国の子どもも熱中！「算数学習ゲーム」

1 ファイル 1.00 KB

ダウンロード

特典映像

谷和樹の解説

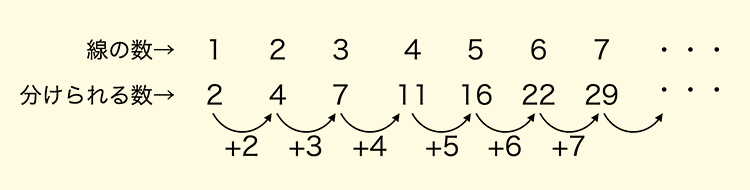
生成AIをつかう高校生たち

高校生に授業しました。
授業っていっても、ほんの数分です。

SDGs QUEST みらい甲子園
https://sdgs.ac/

というイベントです。

TBS系のプロダクションが運営していました。
当然、台本があります。
ただ、私の場合は教師なので。

台本はさておき

という感じになりがちです。
これは、若い頃から向山に叩き込まれました。

指導案を見ながら授業をするな。

ということです。

役者が台本を見ながら芝居をするか。

しないだろう。
教師も同じだ。
そう教えられました。

１　準備は綿密にする。
２　しかし、授業ではその準備を捨てる。
３　子どもたちとのインタラクションを大切にする。

そうやって仕事をしてきました。
だから、どうしても、それが出てしまいます。
もちろん台本にそってやるよう努力はします。
デタラメだと迷惑がかかりますし。

イベントの進行はTBSの藤森アナウンサーでした。
https://www.tbs.co.jp/anatsu/who/fujimori.html
ゲストはモデルのトラウデン直美さん。
https://ameblo.jp/trauden-naomi/
お２人も、私と同じだったと思います。
その場での流れを大切にされているようでした。

授業したテーマはこれです。

生成AI

最初にプロデューサーから示されたのは

ディープフェイク

です。
これを２〜３分で教えるのです。
２〜３分ですよ。
あなたなら何を教えますか。
今回はこの動画生成AIを取り上げました。

Sora

東京の街を歩く女性の動画です。
とても有名になったやつです。
これを見せて、高校生に意見を聞きました。
高校生の観察力と頭脳。
柔らかいですねー。
動画の女性の

・歩き方
・表情

などに直感的な違和感をもったようです。
動画の最初と最後で

・女性の髪型
・女性の服

などの微妙な違いがある。
それも、すぐに見つけていました。
そのうえで、

いずれ、

このような違和感はなくなっていく。

ということ。
つまり、

人間の目では見破れなくなる。

その可能性が高いことを話しました。
だからこそ、

新しい情報をみたときの裏付け

あるいは

情報を使うときの倫理観

などが大切になるということ。
それを話して終わりです。

さて、その後です。
高校生たちに

生成AIを使った活動

をしてもらいました。
自分たちが考えたSDGs企画。
そのプロモーションを考えるのです。
ChatGPTを活用しながら、

よりよいプロモーションを考えよう

という活動です。
「プロモーション画像」なども生成させます。
たった10分ほどです。
これが面白かった。
最初は悩むグループもありました。
ChatGPTに何を命令しようか、と悩むのです。

１　「よい命令」とか考えなくていいよ。
２　最初は「ざっくり」聞いていい。
３　その答えをみて、また聞き直せばいい。
４　どんな命令を何回しても生成AIは嫌がらない。
５「やりとり」をどんどんしてみよう

そんな感じでアドバイスしました。
あっという間でしたね。
慣れるのが。
生成AIを初めて使う子がほとんどだったのですが。
ゲーム的な感覚に優れているのでしょうか。
どんどん命令しては、次々に修正していました。

１　まず、やってみる。
２　結果がでる。
３　また、やってみる。
４　また結果がでる。
５　傾向をみて、もっといい命令を考える。

みたいな感じです。
どんどん積極的に使うチーム。
あるいは、ちょっと生成AIに懐疑的なチーム。
いろんなスタンスの子がいるのも楽しかったです。
それぞれが、それぞれの使い方を論理的に考えている。
そんな様子でした。

1　向山の学習ゲームの授業

たかがゲーム。
されどゲームです。
授業にゲームを取り入れる。
それは非常に効果的です。
たとえば、

習熟型

のゲーム。
ビンゴ系とか、カルタ系とか。
知らないうちにたくさん練習してしまうタイプです。

あるいは

論理型

のゲーム。
一見簡単そう。
でも、なかなかできないヤツです。

例えば、
「ケーニヒスベルクの橋」
とか。
代表例ですよね。
ご存知でしょうか。

ドイツにケーニヒスベルクという街がありました。
その街には川が流れていました。
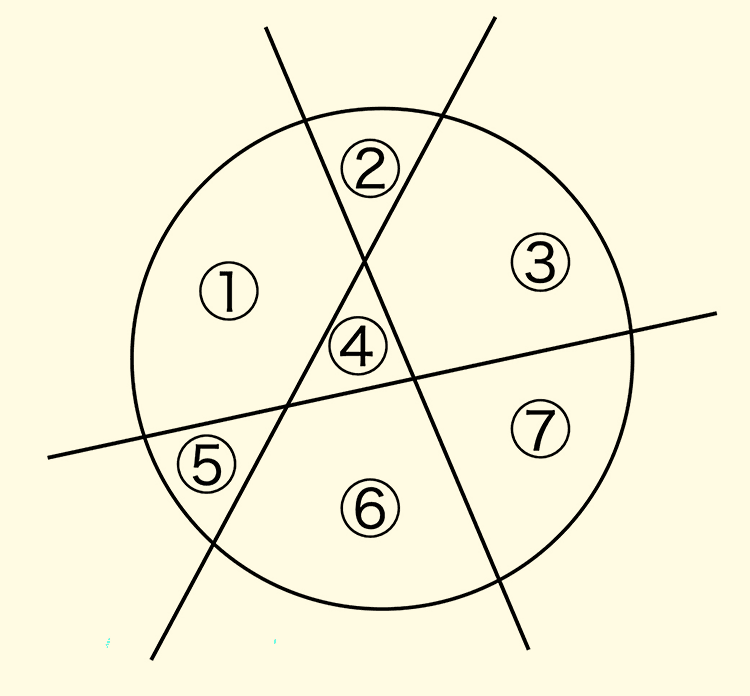
その川には７つの橋がかけられていました。
あるとき、町の人が次のようにいいました。

「この川にかかっている７つの橋を、全部わたって元のところに返ってくることはできるか。ただし、同じ橋は２度通れない」

その川と橋は下の絵のようになっていました。

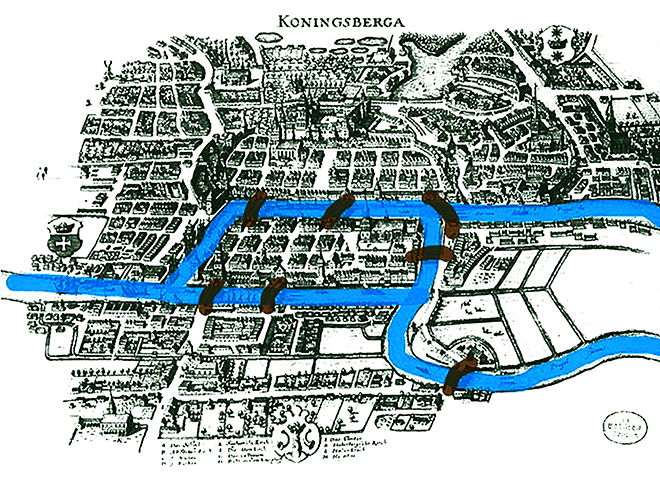
(https://note.com/yukionoguchi/n/n33f4c71b94c8)

これもかつて、向山が授業で扱った問題です。
こういうゲーム的な問題。
ゲームというよりパズル的かも知れません。
子どもたちの論理的思考力を高めます。

さて、この橋の問題は、今回は扱いません。
また、いずれ。
今回は、向山が上海でやった授業を取り上げます。
授業の題材は「学習ゲーム」です。

２　向山の授業の導入

授業の導入。
中国の子どもたちです。
初対面です。
向山は
「こんにちは」
とだけ言うと、前置きなく板書します。

向山洋一

「読んでみて下さい」
と指示し、読ませます。
子どもたちは中国語で読んでくれます。

「シャン、シャン、ヤン、イー」
向山は、だまって「向山」のところをなぞります。
「シャン、シャン」
ここまで、

向山の言葉が非常に少ない

ことが分かりますね。
最小限の指示で授業が進んでいます。
こうした

「研かれた言葉」

が、授業をクッキリさせます。
スピード感を生みます。

その後、２つ板書します。

学習game
遊戯学習

そして
「分かりますか」
「意味が分かりますか」
と発問します。
向山は
「ゲーム」
という概念を出したかったのでしょう。
ところが、挙手した女の子。
ちょっとだけ予想外の反応をします。

楽しく勉強できる

この反応に対して、私なら
「そうだね、"ゲーム"ということだね」
とか、言ってしまいそうです。
向山は、そうしません。
女の子が
「楽しく勉強できる」
と言った瞬間、即座にです。

算数の勉強を楽しくしていきたいと思います。

と、その子の発言を

100%引き取って対応する

のです。
このあたりが、なかなかマネできないところです。

３　円を分ける

さて、本題です。
これは、向山の「超有名」な授業です。
知っている人もいるかも知れませんね。
でも、です。
今回、
あらためて、
その授業運びをみてみましょう。
なぜなら、

今回の授業は、より分かりやすい

からです。

「中国の子どもたち」への授業

だからです。
外国の子どもです。
言葉が通じません。
より分かりやすく、
よりシンプルに、
授業する必要があるのです。

まず、最初の発問です。

【発問１】
ここに丸い円があります。
一本線を引くといくつに分かれますか。

「円」ではありません。
「丸い円」と言っています。
円は丸いに決まっているじゃないかって？
そりゃそうですが。
これは
「イメージ補助」
をしているんです。
例えば、

「楕円」でなくて
「少し長い楕円」

「ひし形」ではなく
「ダイヤのひし形」

「四角」ではなく
「カクっとした四角」

それぞれ、

ちょっとだけイメージを追加

しているわけです。
いつも、こういうことを言うのではありませんよ。
１）目の前の子どもたちを見て、
２）その実態をとらえて、
３）必要に応じて、
加えるのです。
向山は板書します。

ここまでは、子どもに全く作業させていません。
「いくつに分かれますか」
と発問し、
「二つです」
と答えさせ、
向山が自分で、線を引いて円を分けたと思います。
※ 私はこの映像をみていませんので、確証はありません。あくまでも私の推定です。

【発問２】
それでは、円があります。
二本線を引くといくつに分けられますか。
ノートに描いて下さい。

今度は「円」とだけ、言いました。
２回目ですから、当然ですね。
「二本線を引くといくつに分けられますか」
向山は円だけを板書したかも知れません。
あるいは、板書せずに、
「円があります」
と空中に指で示しただけの可能性もあります。
どちらも、効果は変わりません。
指で示しただけのほうが、スピード感はあります。
そして、

作業指示

をするのです。
「ノートに描いて下さい」
ですね。
最初の発問は、教師が描く。
次は、子どもたちに描かせる。
ただし、それほど難しくない、という組み立てです。
さて、ここからです。
すごいのは・・・
向山は、子どもを指名していきます。

書けている子を当てたのでしょう。
一人の子どもが答えます。
「二本の線で四つに分かれます。」
向山は板書します。

「１、２、３、４、四つに分かれますね」
そして、さらに聞きます。
「でも、他に分かれた人がいるはずです」
ここで、おそらく何名かが挙手したでしょう。
挙手した一人を当てます。
「三つに分かれました」
向山は板書します。

板書しながら言います。
「三つに分かれますね。
　これは三つに分かれますね」
そして、この後です。
ここがポイントです。
当たり前のようなのですが、ポイントです。
経験の少ない先生はおそらく見逃します。
私も最初は見逃していました。

これは二つできるんですねえ。
二つとも考えついた人がすごいんです。
よく考えて答えて下さいね。

この言葉です。
この言葉がポイント中のポイントなのです。

最初の発問１を「例示」といいます。

【発問１】
ここに丸い円があります。
一本線を引くといくつに分かれますか。

教師が見せて、例を示しているのです。
簡単なので、子どもには「作業」させていません。

そして、次の発問２。
これは、いわば「助走」です。

【発問２】
それでは、円があります。
二本線を引くといくつに分けられますか。
ノートに描いて下さい。
（ノートに描かせる）
（二種類発表させる）
これは二つできるんですねえ。
二つとも考えついた人がすごいんです。
よく考えて答えて下さいね。

この最後の４行まで含めて「助走」なのです。
これがあるから、だからこそ、
次の発問３が生きるのです。

発問３
一つ多い。
今度は三本です。
はい描いて下さい。

「指示」のように見えますね。
でも、発問です。

一つ多い。
今度は三本です。

の部分が「発問」です。
正確には

一本多くします。
今度は三本です。
いくつに分けられますか。

と発問しているわけです。
ですが、「例示」と「助走」がありましたから、
丁寧に言う必要がありません。
極限まで言葉を削っているわけです。
だから心地よいリズムとテンポが生まれます。
そして、この後の展開は当然こうなります。

いくつ描けたかを聞く。

さっきの「助走」で
「二つとも考えついた人がすごいんです。
　よく考えて答えて下さいね」
と言ったのが伏線になっているのです。
そこで、子どもたちに手を挙げさせます。
このように手を挙げさせることを

分布をとる

と言います。

まずは、
「答えが一つだけあった人」
挙手した子がいたでしょう。
ですが、ここでは人数を数えません。
これを数えたら、その子たちが目立ってしまいます。
あえて数えないのです。

次に、
「答えが二つあった人」
これはたくさんの人が手を挙げました。
だから、今度はあえて数えます。
28人いたわけです。
全員、答えが不十分です。
それが28人もいる。
だからこそ、しっかりと数えておくのです。

「答えが三つあった人」
それが８人。

「四つあった人」
ほとんどいなかったのでしょう。
これも、数えません、
向山は

ちょっと考えてごらんなさい

と投げかけます。
ここで、おそらく少し「間」をとったでしょう。
しばらくして、子どもたちに板書させます。
子どもに板書させる。
ということは、ここからがメインなのです。

子どもからは次の６種類が出ます。

さて、ここで、ふつう、どうしますか？

三本の直線で分ける方法はもっとありますよ

とか

本当にこれだけかな？

とか
言ってしまうのでは？
実際、三本の線では最高７つに分けられます。
この分け方ですね。

ネットでも紹介されているこの授業。
それらも、ここで「７つ」まで示しています。
（関連リンク１，２参照）
もちろん、それでもいいのです。
子どもたちから「７つ」の意見が出ることもあります。
向山のこの授業では、たまたま
「子どもたちから出なかった」
わけです。
そのとき、向山はどうしたでしょうか。

なんと、

そのまま放置する

のです。

いろんな描く方法がありましたけど、
四つの作り方、
五つの作り方、
これもこれも五つですね。
六つの作り方といろいろありました。

板書を指で指し示しながら、このようにまとめます。
なんと、
「いろいろありました」
だけです。
そして、そのままで「発問４」に進んでしまうのです。

そして、です。
一気に
「11個」の人までの「分布をとる」のです。
こういう感じです。

そして、最後の最後。
四本の線のまとめのところで、

なぜ11になるのかの「説明の検討」

をするわけです。
整理します。

１　例示（円を線で分けるよ）
２　助走（数種類の答えがあるよ）
３　本題１（何種類できたかな）
４　本題２（どうやって説明するのかな）

こういう組み立てになっているわけです。
実に巧みだなと思います。
今月は付録がついているようです。
ぜひ、みなさんも分析してみてください。

ちなみに。
この円を線で分けられる数は

２、４、７、11、16・・・

って進むので

階差数列

になってます。

こんな感じですね。
なので、
線の数をaとすると、円の分けられる数は

で、求められます。

※なお、今回は『教育トークライン』1998年8月号に掲載された「テープ起こし」の情報のみで分析しました。
もし、この授業の「音声」とか「映像」とかを見た場合には、また違った分析になるかもしれません。
念のため。

出典・引用文献
１）『教育トークライン1998年8月号』（東京教育技術研究所）p.10-20　向山実物資料A05-246-01
２）『教室ツーウェイ1998年7月号』（明治図書）p.5
３）６年児童ノート「円と直線」多摩川小1999　向山実物資料A05-28-01

関連リンク
１）「円を線で分ける」の授業（TOSSランド）
https://land.toss-online.com/lesson/aapmpuclep7nmpjm
２）「円を分ける」（TOSSランド）
https://land.toss-online.com/lesson/cfBf5Oy6jp6Umw4i2n6N

また、当メルマガで配信している様々な情報については、谷本人の実践、体験、見聞をもとにしておりますが、効果を100パーセント保証する訳ではございません。
選択に当たってはご自身でご判断ください。

※特典資料ダウンロードページおよび資料や映像、音声は予告なしに削除・変更されることがありますこと、あらかじめご了承ください。